ლევ პონტრიაგინი (1908-1988) – მეოცე საუკუნის ერთ-ერთი ყველაზე გამორჩეული მათემატიკოსი, რომელმაც 14 წლის ასაკში სრულად დაკარგა მხედველობა. მიუხედავათ ამისა, მან მნიშვნელოვანი ცვლილებები შეიტანა ალგებრულ და დიფერენციულ ტოპოლოგიაში, ვარიაციულ მეთოდებსა და მართვის თეორიაში.

ამ გენიალური მეცნიერის სახელთან დაკავშირებულია მთელი ეპოქა მათემატიკური მეცნიერებების განვითარების ისტორიაში. პონტრიაგინის გენიალური იდეები დიდწილად განსაზღვრავდა მე-20 საუკუნის მთლიანი მათემატიკის განვითარების მიმდინარეობას. ეს ყველაფერი ვერ მოხდებოდა, რომ არა მისი დედის მიზანდასახულობა და უსაზღვრო რწმენა შვილის მიმართ. ასევე, ლიოვას მისი კლასელი-მეგობრებიც დაეხმარნენ. ბიჭის ცხოვრება სამუდამოდ გაიყო ორ ნაწილად, როცა ჩვეულებრივი ოჯახის ყოველდღიური წყნარი ყოფა საშინელმა ტრაგედიამ დაარღვია…

ლიოვა დაიბადა 1908 წლის 21 აგვისტოს, მოსკოვში. ის დაინტერესებული იყო ტექნიკით და ინჟინრობაზე ოცნებობდა. როცა ლიოვას 13 წელი შეუსრულდა, მათი ოჯახის მშვიდ ცხოვრებას ტრაგედია ეწვია. ბიჭმა საშინელი ტრავმები მიიღო პრიმუსის აფეთქების შედეგად. სახე დამწვარი ჰქონდა, განსაკუთრებით კი თვალები დაზიანდა. ქირურგიული ჩარევის მიუხედავათ ლიოვამ სამუდამოდ და გამოუსწორებლად დაკარგა მხედველობა. რაიმე იმედი, რომ თუნდაც ნაწილობრივ შეძლებდა თვალისჩინის დაბრუნებას, აღარ დარჩა.

მან სკოლაში სიარული შეწყვიტა. რამდენიმეკვირიანი გაცდენების შემდეგ კლასელებმა, მასწავლებლის რჩევით, ის სახლში მოინახულეს. კარი მათ აცრემლებულმა დედამ გაუღო და სამწუხარო ამბავი აცნობა: “ლევი თქვენთან ერთად ვეღარ ისწავლის. მას ოპერაცია გაუკეთეს, თუმცა უშედეგოდ, ის დაბრმავდა და სკოლაში სიარულს ვეღარ შესძლებს”. წუთიანი სიჩუმის შემდეგ, ბავშვებისგან ინიციატივა წამოვიდა: — “ჩვენ მას რიგრიგობით გავყვებით სკოლაში”, “სახლშიც მოვაცილებთ”, “გაკვეთილებსაც მოვამზადებინებთ”, “მე ხვალ გაგყვები სკოლაში”; “მე მოგიყვები რა გავიარეთ ალგებრაში”; – მეგობრები ერთმანეთს არ აცლიდნენ ლაპარაკს. მეგობრებმა შეადგინეს გეგმა, თუ ვინ რომელ დღეს წაყვებოდა სკოლაში ლევს, ვინ რას აუხსნიდა. სკოლაში, ლევის გვერდზე მჯდომი კლასელი, გაკვეთილის მსვლელობისას, ხმადაბლა ეჩურჩულებოდა, თუ რას წერდა მასწავლებელი დაფაზე. კლასში სიჩუმე იდგა, როცა ლევი გაკვეთილს ყვებოდა. როგორ უხაროდათ ბავშვებს მისი წარმატება და კარგი ნიშნები!

ლიოვას მამამ ვერ გადაიტანა შვილის ტრაგედია. იგი თანდათან უფრო და უფრო მეტად დასნეულდა და 1927 წელს ინსულტის შედეგად გარდაიცვალა. დედა დარჩა მარტო – ტკივილთან და შვილის უმწეო მდგომარეობასთან პირისპირ. თუმცა ქალი არ დანებდა. ქვრივი მთელი ძალებით ცდილობდა შვილისთვის რაც შეიძლება ბედნიერი ცხოვრება შეექმნა. მიუხედავად იმისა, რომ მათემატიკაში განათლება არ ჰქონდა, მან ლიოვასთან ერთად დაიწყო ამ მეცნიერების შესწავლა, რათა დახმარებოდა უნივერსიტეტში ჩაბარებაში. დედისა და შვილის მიზანდასახულობამ შედეგი გამოიღო — ლიოვამ სკოლა ოქროს მედლით დაამთავრა და წარმატებით ჩააბარა ყველა გამოცდა, რის შედეგადაც ფიზიკა-მათემატიკის ფაკულტეტის სტუდენტი გახდა.

მეორე კურსზე გადასვლისთანავე მას უკვე სერიოზული მათემატიკური ნაშრომები ჰქონდა. 22 წლის ასაკში ლიოვა თავისი უნივერსიტეტის ალგებრის კათედრაზე დოცენტის თანამდებობაზე დაინიშნა. ამასთან ერთად, იგი მათემატიკისა და მექანიკის სამეცნიერო-კვლევით ინსტიტუტშიც მოღვაწეობდა. 27 წლის ასაკში კი ახალგაზრდა მეცნიერს ფიზიკა-მათემატიკის მეცნიერებათა დოქტორის ხარისხი მიენიჭა.

1937 წელს პონტრიაგინმა წარმოადგინა ნაშრომი დინამიკურ სისტემებზე. იმავე წელს გამოიცა მისი სამეცნიერო სტატია სახელწოდებით „სტრუქტურულად მდგრადი სისტემები“, რომელიც საფუძვლად დაედო დინამიკური სისტემების ფართო თეორიის ჩამოყალიბებას.

ლევ პონტრიაგინმა განსაზღვრულად მნიშვნელოვანი წვლილი შეიტანა ტოპოლოგიის განვითარებაში. მან გააერთიანა ალექსანდერის დუალობის კანონი და მის საფუძველზე შეიმუშავა უწყვეტ ჯგუფთა ხასიათების (ფუნქციების) თეორია (პონტრიაგინის ხასიათები), მიაღწია მაღალ შედეგებს ჰომოტოპიათა თეორიაში და განსაზღვრა კავშირები ბეტის ჯგუფებს შორის. ასევე, პონტრიაგინმა განახორციელა რამდენიმე აღმოჩენა რელაქსაციური რყევების ასიმპტოტიკაში.

მეცნიერი განსაკუთრებით დაინტერესდა ავტომატური რეგულირების თეორიით, რომლის საფუძველზეც ჩამოაყალიბა ოპტიმალური მართვის თეორია. მასვე ეკუთვნის დიფერენციული თამაშების თეორიის დამუშავებაც.

გენიალური მეცნიერი გარდაიცვალა 1988 წლის 3 მაისს, 79 წლის ასაკში.

დიფერენციული თამაშები — მართვის მათემატიკური თეორიის ქვედარგია, რომელიც ობიექტის მართვას კონფლიქტურ სიტუაციებში იკვლევს. დიფერენციული თამაშები ასევე თამაშთა თეორიაშიც განიხილება. დიფერენციულ თამაშებში მოთამაშეთა შესაძლებლობები აღწერილია დიფერენციული განტოლებებით, სადაც შემადგენელი სიდიდეები – მართვის ვექტორებია, რომლითაც მოთამაშეები სარგებლობენ. სტრატეგიის შერჩევისას თითოეული მოთამაშე ეფუძნება მხოლოდ მიმდინარე ინფორმაციას სხვა მოთამაშეთა ქცევის შესახებ. განასხვავებენ ორი მოთამაშისა და მრავალი მოთამაშის დიფერენციულ თამაშებს.

დიფერენციული თამაშებიდან ყველაზე საფუძვლიანად შესწავლილია დადევნების თამაში, სადაც ორი მოთამაშეა: ერთი — მდევარი, მეორე — გაქცეული. მდევრის მიზანია ვექტორი Z(t) გარკვეულ M სიმრავლეში რაც შეიძლება მალე გადაიყვანოს; ხოლო გაქცეულის მიზანია მაქსიმალურად შეაფერხოს ამ ვექტორის M-ში მოხვედრის დრო.

დიფერენციულ თამაშებში ფუძემდებლური შედეგები მიღებულ იქნა 1960-იან წლებში — ლ. პონტრიაგინის, რ. აიზეკსის, ლ. ბერკოვიცის, უ. ფლემინგის და სხვათა მიერ.

ერთ-ერთი პირველი, ვინც დიფერენციული თამაშების კვლევა დაიწყო, იყო რუფუს აიზექსი (მისი ნაშრომი 1951 წლით თარიღდება, თუმცა პირველად 1965 წელს გამოქვეყნდა). ხოლო პირველი თამაში, რომელიც მან გააანალიზა, იყო ე.წ. „მკვლელი მძღოლის ამოცანა“. აღსანიშნავია, რომ თავად აიზექსი, „მძღოლისა“ და „ქვეითის“ ნაცვლად ტორპედოსა და მისგან თავის დაღწევის მსურველ პატარა კატერს გულისხმობდა.

თამაშთა თეორიაში, მკვლელი მძღოლის ამოცანა წარმოადგენს დევნის მათემატიკურ ამოცანას, სადაც წარმოსახვითი გაქცეული „ქვეითი“ მოძრაობს ნელა, მაგრამ მანევრულად, ხოლო მდევარი „მძღოლი“ ბევრად უფრო სწრაფია, თუმცა მანევრებში შეზღუდული. ვარაუდობენ, რომ არც ერთი არ იღლება — ისინი დაუსრულებლად აგრძელებენ მოქმედებას. თამაშის მთავარი კითხვაა: რა პირობებში და რა სტრატეგიით შეძლებს მძღოლი გაქცეულის დაწევას, ან შეძლებს თუ არა გაქცეული დაუსრულებლად აარიდოს თავი შეჯახებას?

ეს ამოცანა დიფერენციული თამაშის კლასიკურ მაგალითს წარმოადგენს — თამაში მიმდინარეობს უწყვეტ დროსა და უწყვეტ სივრცეში. მისი გადაწყვეტისთვის მათემატიკური ჩარჩოს სახით შეიძლება გამოყენებულ იქნეს ვარიაციული აღრიცხვის მეთოდები. მიუხედავად იმისა, რომ ამოცანა თავიდან გასართობად შეიძლება მოგვეჩვენოს, ის მათემატიკოსებისთვის მოდელირების სერიოზულ ამოცანას წარმოადგენს, რომელსაც რეალურ ცხოვრებაშიც აქვს გამოყენება — მაგალითად თავდაცვაში, ავიაციასა და რობოტიკაში.

აღსანიშნავია, რომ ამ ამოცანის დისკრეტული ვერსია აღწერილი აქვს მარტინ გარდნერს. განვიხილოთ შედარებით მარტივი, თუმცა „მკვლელი მძღოლის“ ამოცანასთან ნაწილობრივ მსგავსი თამაში — „საპატრულო მანქანა“.

ამ სცენარში საპატრულო პოლიციის მანქანა იმყოფება ქალაქის ერთ-ერთ გზაჯვარედინზე. ქალაქს აქვს სწორხაზოვანი, ოთხკუთხა გეგმარება. ქალაქში ასევე მოძრაობს მეორე მანქანა — დანაშაულში მხილებული პირებით. პოლიციის მანქანა ორჯერ უფრო სწრაფია, ვიდრე დამნაშავეთა მანქანა, მაგრამ პოლიციელებს მოძრაობის წესების დაცვა უწევთ, რომელთაც დამნაშავეები სრულიად უგულებელყოფენ. საგზაო წესები პოლიციის მანქანას უკან მიბრუნებასა და მარცხნივ მოხვევას უკრძალავს, რის გამოც პოლიციელებს ნებისმიერ გზაჯვარედინზე მხოლოდ ორი ვარიანტი აქვთ: სვლა პირდაპირ განაგრძონ ან მარჯვნივ მოუხვიონ. დამნაშავეთა მანქანას კი შეუძლია ოთხი მიმართულებიდან ნებისმიერი ერთ-ერთი არჩევა.

ამ თამაშის დისკრეტულ მოდელში ქალაქის გზაჯვარედინები წარმოდგენილია უსასრულო უჯრედებიან დაფად, როგორც ჭადრაკის დაფაა. პოლიციის მანქანა მცრე ფიგურაა, რომელზეც მითითებულია ისრით მოძრაობის მიმართულება, ხოლო დამნაშავეთა მანქანა — ჩვეულებრივი ფიგურაა.

• მოთამაშეები მორიგეობით აკეთებენ სვლებს, პირველ სვლას პოლიციის მანქანა აკეთებს.
• მოძრაობა მხოლოდ სწორხაზოვნად შეიძლება — ზემოთ, ქვემოთ, მარჯვნივ ან მარცხნივ, მაგრამ არასოდეს დიაგონალზე.
• დამნაშავეთა მანქანა თითო სვლაში ერთ უჯრაზე გადადის, პოლიციის მანქანა — ორ უჯრაზე.
• პოლიციის მანქანამ სვლა ან პირდაპირ უნდა გააგრძელოს, ან მარჯვენა მოხვევით გააკეთოს (ერთ სვლაში: ჯერ მოხვევა და მერე ორ უჯრაზე გადაადგილება). ანუ, მარჯვნივ მოხვევა და შემდეგ ორი უჯრის გავლა — ერთდროულად უნდა განხორციელდეს. ერთ უჯრაზე გადაადგილება, მარჯვნივ მოხვევა და შემდეგ კიდევ ერთ უჯრაზე გადაადგილება – ერთ სვლაში დაუშვებელია.
დაჭერად ითვლება ის მომენტი, როცა პოლიციის მანქანა ხვდება რომელიმე იმ 8 უჯრაზე, რომლებიც დამნაშავეთა მანქანის უჯრის მიმდებარედაა, მეზობლად — ზემოდან, ქვემოდან, გვერდიდან ან დიაგონალზე.

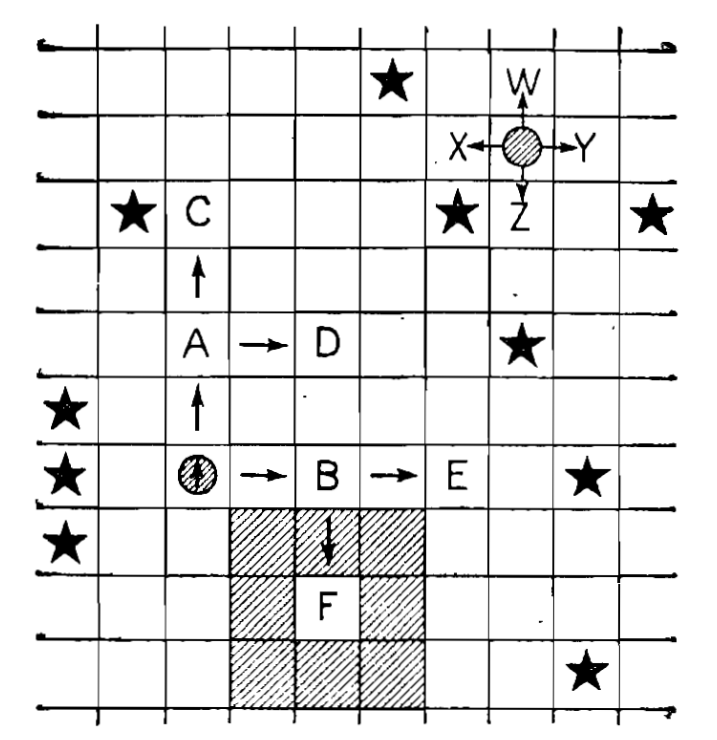
თამაშის წესები ნათლადაა წარმოდგენილი ილუსტრაციაზე. პოლიციის მანქანას (რომელიც დაშტრიხულ წრეში ჩასმული ისრითაა ნაჩვენები) უკვე პირველ სვლაში შეუძლია გადავიდეს უჯრა A ან B-ზე. უჯრა A-დან მას შემდგომ შეუძლია გადავიდეს C ან D უჯრაზე, ხოლო B-დან — E ან F-ზე. (თითოეული სვლის შემდეგ ფიგურა, რომელიც პოლიციის მანქანას განასახიერებს, საჭიროების შემთხვევაში, ბრუნდება ისე, რომ ისარი მიუთითებდეს იმ მიმართულებას, რომლითაც მანქანა მოძრაობდა). დანაშაულში მხილებული პირების მანქანას (რომელიც დაშტრიხული წრის სახითაა ნაჩვენები) შეუძლია გადავიდეს უჯრებზე W, X, Y და Z. მაგალითად, თუ პოლიციის მანქანა იმყოფება F უჯრაზე, ხოლო დამნაშავეთა მანქანა — ამავე უჯრაზე ან რომელიმე იმ რვა მიმდებარე უჯრაზეა (ილუსტრაციაზე დაშტრიხულია), ისინი დაჭერილად ჩაითვლებიან.

რომელ უჯრაზე უნდა იმყოფებოდეს პოლიციის მანქანა, რათა დამნაშავეების მიერ თავის დაღწევა შეუძლებელი გახდეს? აიზექსი თავის ნაშრომში აჩვენებს, რომ იმ უჯრის გარშემო, სადაც საწყის მომენტში იმყოფება პოლიციის მანქანა, შესაძლებელია ასიმეტრიული, კომპაქტური არეს აგება, რომელიც შედგება 69 უჯრისგან. არ აქვს მნიშვნელობა, ამ არეს რომელ უჯრაზე იმყოფება თამაშის დასაწყისში დამნაშავეთა მანქანა — მისი ბედი წინასწარ განსაზღვრულია. სწორია პირიქითადაც — თუ დამნაშავეთა მანქანა საწყის მომენტში იმყოფება აღნიშნული არეს გარეთ, მას ყოველთვის ექნება შესაძლებლობა დაუსჯელად გაექცეს მდევარს. (გაითვალისწინეთ, რომ დაფა განიხილება როგორც უსასრულო.)

სცადეთ დამოუკიდებლად იპოვოთ ეს 69 დამღუპველი უჯრა. ამისათვის გჭირდებათ 50×50 უჯრიანი დაფის დახაზვა და პოლიციის მანქანის განთავსება ცენტრში. შემდეგ დაიწყეთ ექსპერიმენტები. სანამ თამაში სრულად არ იქნება გაანალიზებული, იგი მრავალი მოულოდნელი სიურპრიზის წყაროდ რჩება. დანაშაულში მხილებულთა „მძღოლი“, საწყისი პოზიციის სხვადასხვა არჩევით, ცდილობს განსაზღვროს, რომელი უჯრებიდან შეძლებს დაფის საზღვრამდე მიღწევას ვიდრე დაიჭერენ.

რა თქმა უნდა, მრავალჯერ თამაშის შემდეგ შესაძლებელია, რომ საბოლოოდ ჩამოაყალიბოთ ის ზონა, რომელიც დამნაშავეთათვის საფრთხის შემცველია. თუმცა არსებობს უფრო მარტივი მეთოდიც — რომელიც არამხოლოდ განსაზღვრავს აღნიშნული ზონის საზღვრებს, არამედ თითოეულ უჯრას დაუკავშირებს შესაბამის რიცხვს, რომელიც მიუთითებს, რამდენ სვლაში დაეწევა პოლიციის მანქანა დამნაშავეს, იმ შემთხვევაში, თუ ორივე მხარე ოპტიმალურად იმოქმედებს.

შესაძლოა განვიხილოთ შედარებით მარტივი ამოცანაც: დავუშვათ, რომ პოლიციის მანქანა თამაშის დასაწყისში იმყოფება უჯრაზე, რომელიც ილუსტრაციაზე აღნიშნულია წრითა და ისრით, ხოლო დამნაშავეთა მანქანა — რომელიმე იმ უჯრაზე, რომლებიც მონიშნულია ვარსკვლავებით. ამ უჯრებიდან ერთის გარდა ყველა საშუალებას აძლევს დამნაშავეს დაუსჯელად გაექცეს მდევარს. რომელია ეს საბედისწერო უჯრა და რამდენი სვლა დასჭირდება პოლიციის მანქანას, რათა დაეწიოს დამნაშავეებს, იმ პირობით, რომ ორივე მხარე ირჩევს ოპტიმალურ სტრატეგიას?